Exercise for Chapter 6: Centrality
Answers
Exercise 1

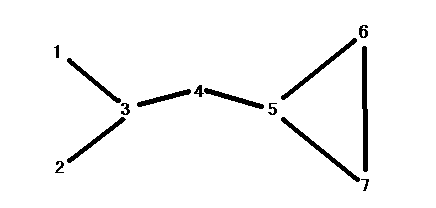
(a) Calculate Degree centrality scores of each node in the network above, and complete the table below.
Degree centrality of a node refers
to the number of edges attached to the node. In order to know the
standardized score, you need to divide each score by n-1 (n = the number
of nodes). Since the graph has 7 nodes, 6 (7-1) is the denominator
for this question.
Degree Centrality
|
|
|
Score |
| 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(b) Calculate Closeness centrality scores of each node in the network above, and complete the table below. (Do not forget to take inverse.)
You need to calculate the inverted
score after you count the total number of steps to a node. In order
to know the standardized score, you need to divide a score by (n-1), then
take inverse. Note that the most central node is node 4 while the
most central node for degree centrality is node 3 and 5.
Closeness Centrality
|
|
|
Score |
| 1 | 1/16 |
|
|
|
1/16 |
|
|
|
1/11 |
|
|
|
1/10 |
|
|
|
1/11 |
|
|
|
1/15 |
|
|
|
1/15 |
|
(c) Calculate Betweenness centrality scores of each node in the network above, and complete the table below.
To calculate betweenness centrality,
you take every pair of the network and count how many times a node can
interrupt the shortest paths (geodesic distance) between the two nodes
of the pair. For standardization, I note that the denominator is (n-1)(n-2)/2.
For this network, (7-1)(7-2)/2 = 15. Note that node 5 has a little
smaller centrality score that node 3 and 4 because the connection between
node 6 and 7 reduces the controllability of node 5.
Betweenness Centrality
|
|
|
Score |
| 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13/45 |
|
|
|
|
|
|
|
|
On the following questions (d),
(e), and (f), you need to remember the lecture by
Motoki. You should read
the brief summary of each centrality on your notes. (I wrote it at the
very end of lecture). If you understand it well, you don't have any
difficulties to answer the three questions.
(d) Suppose the above
network refers to friendship network. Each node represents a person,
and each edge represents friendship between the persons at ends.
If you are interested in finding the most poplar person in the network,
which centrality measure is the most appropriate? Give the answer
with reasons why it is the most appropriate.
The most popular person should
have the highest number of friends. Thus, degree centrality is the
most appropriate measure.
(e) Suppose the above
network refers to information flow network of an organization. Each
node represents a section in the organization, and each edge represents
a possible information exchange between the sections at ends. If
you are interested in finding the section that can most efficiently
obtain information from every other section, which centrality measure
is the most appropriate? Give the answer with reasons why it is the
most appropriate.
To obtain information, one should
be near from everyone. In this sense, the node in the nearest position
on average can most efficiently obtain information. Thus, closeness
centrality is the most appropriate.
(f) Again, suppose the above network refers to information flow network of an organization. If you are interested in finding the section that can most frequently control information flow in the network, which centrality measure is the most appropriate? Give the answer with reasons why it is the most appropriate.
To control information flow,
a node should be between other nodes because the node can interrupt infromation
flow between them. Thus, betweenness centrality is the most appropriate
measure.
Exercise 2
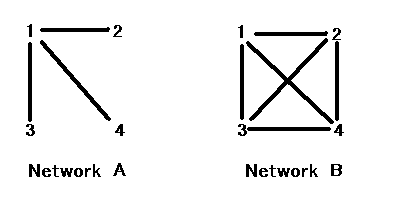
(a) For each Network, calculate the three centrality indexes (degree, closeness, and betweenness) for each entire graph (Not for each node of a graph) . Which graph is more centralized ?
Use equations 6.8, 6.9, and 6.10 on Page 171 in the textbook for this question. The basic idea of centrality for entire graph is to calculate average deviance of each node from the most central node.
Degree centrality (Equation 6.8)
Network A
Node 1 - centrality score
3
Node 2 - centrality score 1
Node 3 - centrality score
1
Node 4 - centrality score
1
The maximum score is 3.
Use Eq.6.8
((3-3)+(3-1)+(3-1)+(3-1))/(16-12+2) = (0+2+2+2)/6 = 1
The degree centrality score of Network A is 1.
Network B
Node 1 - centrality score
3
Node 2 - centrality score
3
Node 3 - centrality score
3
Node 4 - centrality score
3
The maximum score is 3.
Use Eq.6.8
((3-3)+(3-3)+(3-3)+(3-3))/(16-12+2) = (0+0+0+0)/6 = 0
The degree centrality score of Network B is 0.
Thus, Network A is more centralized
than Network B for degree centrality.
Closeness centrality (Equation
6.9)
* You need to use standardized
score.
Network A
Node 1 - centrality score
3/3 = 1
Node 2 - centrality score
3/5
Node 3 - centrality score
3/5
Node 4 - centrality score
3/5
The maximum score is 3/3 = 1.
Use Eq.6.9.
((1-1)+(1-3/5)+(1-3/5)+(1-3/5))/((16-12+2)/(8-3))
= (0+2/5+2/5+2/5)/(6/5)
= (6/5)/(6/5) = 1 .
The closeness centrality score of Network A is 1.
Network B
Node 1 - centrality score
3/3 = 1
Node 2 - centrality score
3/3 = 1
Node 3 - centrality score
3/3 = 1
Node 4 - centrality score
3/3 = 1
The maximum score is 1.
Use Eq.6.9.
((1-1)+(1-1)+(1-1)+(1-1))/((16-12+2)/(8-3)) = (0+0+0+0)/(6/5) = 0
The closeness centrality score of Network B is 0.
Thus, Network A is more centralized
than Network B for closeness centrality.
Betweenness centrality (Equation
6.10)
* You need to use standardized
score.
Network A
Node 1 - centrality score
3/3 = 1
Node 2 - centrality score
0
Node 3 - centrality score
0
Node 4 - centrality score
0
The maximum score is 3/3 = 1.
Use Eq.6.10.
((1-1)+(1-0)+(1-0)+(1-0))/(4-1) = (0+1+1+1)/3 = 1.
The closeness centrality score of Network A is 1.
Network B
Node 1 - centrality score
0
Node 2 - centrality score
0
Node 3 - centrality score
0
Node 4 - centrality score
0
The maximum score is 0.
Use Eq.6.10.
((0-0)+(0-0)+(0-0)+(0-0))/(4-1) = (0+0+0+0)/3 = 0
The closeness centrality score of Network B is 0.
Thus, Network A is more centralized than Network B for betweenness centrality.
I note that centrality score
of Network A is 1 for any centrality measures while centrality score of
Network B is 0 for any centrality measures because Network A is the maximally
centralized network with four nodes and Network B is the non-centralized
network with four nodes.
(b) Comparing the centralized and non-centralized graph above, discuss advantages and disadvantages of centralized network.
This is an open-ended question.
The aim of the question is to let you imagine some centralized and non-centralized
networks in the real world and compare them. Since this course is
a sociology course, it is important that you apply the mathematical approach
to actual social phenomenon. I give you a sample answer.
A Sample Answer
If the network represents information
flow, Node 1 in Network A has huge controllability of information flow.
If node 1 works very well, the network is very efficient because there
is no redundant edges in the network. However, if node 1 does not
work, node 2, 3, and 4 are isolated. In this sense, Network A is risky
in that efficiency of information flow totally depends on node 1's performance.
On the other hand, Network B is more flexible. Even if node 1 does
not work, all other nodes can still communicate one another. However,
in another sense, this network has many redundant edges. If it takes
costs to make edges, this network is very costly.
Exercise 3
Centrality can be used
as an index of power in networks, because the most central node is more
likely to occupy the most powerful position. Do you think it is true ?
Answer with reasons why you think so.
The answer is actually
"no". An experimental study by Cook et. al. (1983) demonstrates that
centrality is not necessarily the index of power. You do not need to know
about this study, but you need to think whether the powerful position is
always central in a network. I do not explain details of this study.
If you are interested in it, contact me. I will explain it. Since
the main purpose of this question is let you think about the meaning of
centrality, you can write your own idea.
If you have questions, ask
Motoki. mwatabe@ucla.edu