December 1999; April 2000

Population Forecasting, Social Construction of Calendar Systems, and other Thoughts for Year 2000

by David D. McFarland

Contents

Earlier Forecasts about 2000

As 1999 turns into 2000, there have been plenty of forecasts about what the next millennium will bring. Here I will do something different, reviewing the forecast I made a couple of decades ago about what things would be like now, and assessing how far wrong I had been.

One of the uses for mathematical models in demography is in forecasting changes in the size and composition of a population. (This and related topics are treated at length in the "Mathematics of Population" course, Soc. 240/197, which I might be offering in winter quarter 2001. These topics are sometimes also touched on in other courses in demography or mathematical sociology.)

Like any other attempts to foretell the future, forecasting future population is risky business. As Phil Hauser used to say, anyone who claims to be able to foretell the future is either a charlatan or a fool. He should perhaps have added, "or both".

Demographers often try to sidestep that risk by protesting that their calculations are not "forecasts", attempts to predict what will actually happen in the future, but instead are "mere projections", nothing more than working out the arithmetic from arbitrary assumptions.

This is not a very convincing ploy, however, since there is little interest in mere projections. Arbitrary assumptions unsuitable for attempts to predict the future are, indeed, important for various uses in technical demography. But those belong in courses and publications addressed to demographers and related specialists, not in public pronouncements aimed at the general reader. The latter wants to know what the future will bring, and to know it beforehand, so that timely preparations can be made.

If for example the number of children will be increasing, that would best be known ahead of time, to allow for timely preparation of more or larger school systems. Similarly, if there will be increases in the number of elderly needing health care, it is best that that be known soon enough to build the needed facilities, train the needed personnel, and find the needed funding for all of it. Those are among the kinds of concerns that create demand for population "forecasts", not "mere projections".

Decades ago, when the year 2000 seemed safely in the future, some of us made predictions about what things would be like then. But the time that was then "then" is now "now", and it is now (or soon will be) possible to compare the 2000 we foresaw with the 2000 now actually arriving. I shall provide my comparison, and invite others to do likewise.

Back in the mid-1970s, I wrote as follows:

At the time of the 1970 United States Census, persons over 65
years of age numbered 20 million and constituted just slightly
less than 10% of the United States population.  However, both
popular news media and scientific journals have recently
published articles containing predictions of remarkable increases
in the numbers and proportions of elderly persons over the course
of the next several decades.  In Time magazine it was
recently stated that "20% of the American population will be
over 65 by the year 2000." .... Constance Holden, writing in
Science, went 5% further, asserting that "People over 65
...will... by the year 2000 constitute an unprecidented 25
percent of the population".

In fact, neither Time's 20% nor Holden's 25% is at all
plausible, given the current age composition of the United States
population and the short amount of time between now and the year
2000.  By the year 2000 the absolute number of persons 65
or older will increase substantially, from 20 million to
approximately 30 million, but the entire population will also
increase substantially, from slightly over 200 million to
somewhere approaching 300 million; therefore, the proportion of
persons 65 and older will remain in the vicinity of 10% --
perhaps 8%, or possibly 12%, but certainly neither 20% nor
25%.

[In the remainder of the chapter I spelled out the basis for my
predictions, using multiple decrement life table calculations,
and discussed some general issues of population projections and
forecasts.]

Followup Assessment

The US Census Bureau provides periodically updated population estimates. At this writing in December 1999, those include estimates for 1 November 1999, sufficiently close to 2000 for present purposes. As 1999 is about to turn to 2000, the census figures are:

Had I had the oracular wisdom to make vague pronouncements, I could now claim great foresight. Rather than "those 65 and older" an oracle would have referred to "the elderly population", a collectivity whose vague boundaries give more flexibility in subsequently squirming out of failed predictions. Similarly, "is unlikely to" would have been more flexible than my "will definitely not".

Hedging is another tool for oracles; making two quite different predictions improves the prospects of turning out to have correctly predicted something. For example, one assertion, "The elderly population is unlikely to grow as dramatically as forecast by Holden, or even Time" might have been followed by a different assertion, "But the elderly will be a very significant part of the 2000 population."

And just to cap it off, an oracle might have tossed in an easy although unrelated prediction, say that the sun would still rise in 2000 (if it doesn't, neither the oracle nor any critics will be around for a post-mortem of the failed prediction!), or possibly (and this is really more about an expansively oriented government than the elderly per se) that the elderly population in 2000 would be an important topic of attention in government and policy discussions.

(Alternatively, an oracle might have produced a 400+ page book of speculation about the year 2000 without even mentioning the elderly, as Herman Kahn did in 1967.)

But back then I utilized multiple decrement demographic models, rather than oracular wisdom, and thus I made a much more specific prediction: that those age 65 and older would constitute around 10% -- perhaps 8% or possibly 12% -- of the US population in 2000.

So my prediction was actually sufficiently specific as to be falsifiable. And in fact the actual proportion, 12.7%, lies outside the 8-12% interval I had specified in the forecast I published back in 1978.

True, it wasn't that far outside my interval, and Yes, my wrong forecast wasn't nearly as badly wrong as those of Time and Holden. Still, I wish that my forecast interval had included the actual value (and that the interval itself had been narrower as well!).

Were you also making forecasts about 2000 back a couple of decades ago? Let me know the specifics: mcfarland@soc.ucla.edu.

How well did your forecasts turn out?

Have you been keeping track of forecasts that other social scientists have made, about what things would be like in 2000?

Here is one such, published in 1962. After reviewing the dramatic improvements over the prior two decades in various aspects of the circumstances of American Negroes (as they were then called), that author wrote: 

...I venture to predict the end of all formal segregation and
discrimination within a decade... The attitude of prejudice might
remain indefinitely, but it will be on the minor order of
Catholic-Protestant prejudice within three decades.  These
changes would not mean that there would be equality between the
races within this time... but the dynamic social forces creating
inequality will, I predict, be practically eliminated in three
decades...
Quick, tell me: Which eminent American sociologist published those predictions back in 1962?

References:

Holden, Constance 1976. "National Institute on Aging: New Focus on Growing Old." Science 193: 1081.

Kahn, Herman, and Anthony J. Wiener 1967. The Year 2000: A Framework for Speculation on the Next Thirty-three Years. New York: Macmillan.

McFarland, David D. 1978. "The Aged in the 21st Century: A Demographer's View." Ch. 1, pages 5-22, in: Jarvik, Lissy F., ed. 1978. Aging Into the 21st Century: Middle Agers Today. New York: Gardner Press.

Rose, Arnold 1962. "Postscript Twenty Years Later." Pages xxvii-xlv in: Gunnar Myrdal 1962. An American Dilemma: The Negro Problem and Modern Democracy. Twentieth Anniversary Edition. New York: Harper and Row. (Quotation from page xliv.)

Time 1976. "The Joy of Aging." Time, 8 November 1976, page 86.

Y2K Foolishness

For April Fools Day, 1999, in order to make sure that at least some of the Y2K doomsaying predictions would come true, I constructed a special abacus that, unlike any of the other abaci used during the past three millennia, has only enough beads to count to 1,999, and would fail whenever a calculation required a number 2,000 or higher. See my humor web page for a photo and instructions.

1972: A Y2K Precursor for Slide Rules?

One of the items in my collection of obsolete computational devices is "The Commercial Calculator", a circular slide rule bearing a 1922 patent date. It was manufactured by Gilson, but is much less common than some other Gilson models (Midget, Binary).

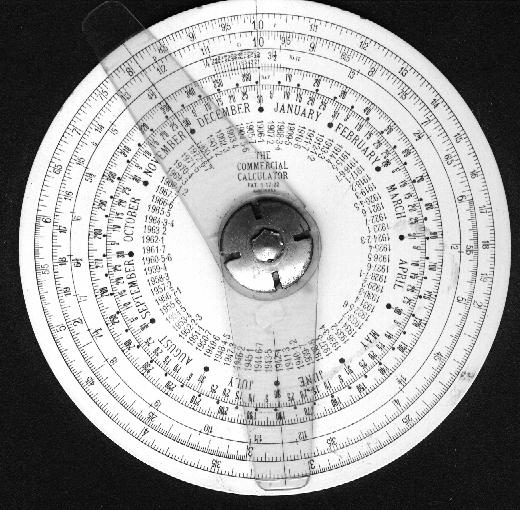
Unlike most slide rules, the Commercial Calculator has specialized capabilities that include calculations pertaining to loans and interest, which in turn require calendrical calculations such as the length of time between two specified dates. Accordingly it includes scales for DayOfYear (1 - 365), MonthAndDay (Jan1 - Dec31), and Year (1900 - 1972).

Here, on the Year scale, we have an earlier counterpart of the Y2K problem (of computers unable to track dates past the year 1999). When this instrument was designed in 1922, its time scale extended 50 years into what was then the future. But this specimen outlived those 50 years; and ever since 1972 it has been, let us say, living on borrowed time.

.

What a coincidence! 1972 happens also to be the year the author of a book on the history of slide rules (Hopp page 159) gives as possibly the last in which Dietzgen (the main Gilson distributor) sold slide rules.

I am sure it was a coincidence, however. The Commercial Calculator itself was an uncommon slide rule, so the fate of the slide rule market did not hinge on it. Furthermore, the vast majority of other slide rules did not have Year scales, nor any other features that would expire on some particular date. It was the advent of affordable electronic hand calculators, not scales truncated at 1972, that brought the demise of slide rules.

My Commercial Calculator is of the slide rule genre. The era which produced such devices began around 1620, when the invention of logarithms by Napier was quickly followed by the development of slide rules through the works of Gunter, Delamain, Oughtred and others. That era lasted more than three centuries, during which a slide rule became a standard tool for students and professionals in science and engineering. That era ended rather abruptly in the 1970s, when the slide rule was replaced by the hand-held electronic calculator. The computational failure of my specimen came from dates going only through 1972.

Perpetual Calendars

In fact, the Commercial Calculator's scales incorporate a kind of perpetual calendar, and someone who understands how those work could go on using it past 1972. It requires a bit of extra effort, but not a great deal -- roughly equivalent to the amount of extra effort required in keeping track of decimal points, a minor inconvenience to which any slide rule user was accustomed.

While the labels on this Calculator stop at 1972, the calendar, of which it represents a segment, continues repetitively, going through a cycle every 28 years (except on some century boundaries; see below). Thus although the scale is marked only from 1900 to 1972, it could be used for any year between 1900 and 2100, simply by subtracting 28 as many times as needed to get a number within the range shown on the scale.

Where does the number 28 come from? Calendars for different years differ in two independent respects, the day of the week on which the year begins (7 possibilities) and whether or not it is a leap year (3 regular years followed by one leap year). Thus in cycling through all those possibilities, the sequence of annual calendars repeats itself after 7x4 = 28 years. (See, e.g., Gould, page 175.)

This fact can be used to apply the Commercial Calculator to years beyond 1972. For example, 1975 is beyond the end of the Year scale, but its calendar is identical to that of 1947, which was 28 years earlier. Similarly, 2010 is beyond the end of the scale, but its calendar is identical to that of 1954, which was 28x2 = 56 years earlier.

But what is special about 1900 and 2100? The solar year is not exactly 365.25 days, and the discrepancies, which cumulate to about 18 hours per century, are handled by omitting February 29 on some of the years at century boundaries, 1900 and 2100 among them (Klein, page 128).

The rule that covers these more complicated adjustments at century boundaries, as well as ordinary leap years, is as follows: (a) Any year not divisible by 4 is an ordinary year, with 365 days. (b) Any year evenly divisible by 4, but not by 100, is a leap year (i.e., gets an extra day, as 29 February). That much of the rule is widely known, for example in the children's rhyme, "Thirty days hath September..." that in fact dates back at least to the year 1488 and the Computus of Anianus (see Smith, vol. 2, page 665) where it appears in Latin form:

Junius aprils september 
     et ipse nouember
Dant triginta dies 
     reliquis supadditur vnus,
De quorum numero 
     februarius excipiatur.
Not so widely known (since it rarely needs to be invoked) is the continuation of the rule: (c) Any year evenly divisible by 100, but not by 400, is not a leap year. (d) Any year evenly divisible by 400 is a leap year. Thus 1900 and 2100 are not leap years, per rule (c); but every fourth year between them is a leap year, per rule (d) for 2000 and rule (b) for the others.

Thus the interval from 1 March 1900 to 28 February 2100 is uninterrupted by special adjustments at century boundaries, and a perpetual calendar with 28 year cycles will work throughout that 200 year interval.

References:

Gould, Stephen Jay 1997. Questioning the Millennium: A Rationalist's Guide to a Precisely Arbitrary Countdown. New York: Harmony Books.

Hopp, Peter M. 1999. Slide Rules: Their History, Models, and Makers. Mendham, NJ: Astragal Press.

Klein, Herbert Arthur 1974. The Science of Measurement: A Historical Survey. New York: Dover.

Smith, David Eugene 1953. History of Mathematics. 2 volumes. New York: Dover.

Further Calendrics

Time, according to some of my fellow sociologists, is a "social construct". True enough. For one thing, calendars are designed by humans, and more often by teams or committees of some sort than by hermits (see e.g. Duncan 1999).

Mathematical sociologists such as myself are less apt to use the term, "social construct", than are some other brands of sociologists. Nevertheless, we in fact engage in a bit of social construction in the ways we treat time. Indeed, we treat time as different social constructs on different occasions, as suits our convenience. Sometimes, akin to old-fashioned clocks and watches with hands that can be adjusted in arbitrarily small increments, we treat time as a continuous variable, t, and put it in such things as differential equations involving dY/dt, the instantaneous rate of change of some other variable, Y. Other times, akin to digital watches and calendars, we treat time as a discrete variable, and analyze change between successive time points such as decennial censuses. Yet other times we generalize away from whatever it is that is measured by clocks and calendars, and use the term "time" for things like successive generations in a family line, which in fact are separated by variable rather than fixed amounts of clock-and-calendar time.

Still, merely labeling time a "social construct" is not enough; it is a bit more complicated than that. In examining various aspects of calendar systems, we shall see that some social constructs are more constrained than others by objective, natural phenomena that exist prior to and independent of whatever further organization humans may try to impose on those phenomena. This is sometimes insufficiently emphasized by social constructionists.

Many different calendar systems have been invented, by groups ranging from Aztecs, Babylonians, Chinese, etc., to Zapotecs (See e.g., Duncan). Furthermore, a given group may have used multiple calendars, either sequentially (e.g., Cowan, chapter 3, on evolution of the Roman calendar) or simultaneously. The Aztecs are sometimes cited as an example of the latter, although it is not entirely clear whether individual Aztecs used both, or whether they were occupation-specific, with priests conducting sacrifices by a 260 day religious calendar but farmers planting maize by a solar year calendar.

(Note: Anyone interested in the Aztec calendars should be aware of Bourgeois who, based on 16th century manuscripts written in the Nahuatl language, claims that Sahagun, who wrote the conqueror's version of Aztec culture, misinterpreted his informants' reports about how they handled the discrepancy between the 365+ days in the sun's period, and the 20x18= 360 days in eighteen 20-day months; and that subsequent authors, unable to read Nahautl and relying directly or indirectly on Sahagun, have perpetuated that misinformation.)

Sometimes time, or some aspect thereof, is conceptualized as cyclical, other times as linear. However, as Zerubavel notes, "those two modes of conceptualizing time are not necessarily mutually exclusive" (page 84). In particular, time in very long cycles (in cases such as the Mayans, whose long cycle was over 5,000 years; Robinson, page 126) is for most purposes indistinguishable from linear time: "Been there, done that" loses much of its force if the time referent is so long ago that memory fades.

Furthermore, not too much should be made of cycles, even ones as short as days and weeks, as supposedly being antithetical to notions such as "progress". The latter is an area where actual mathematics is more adequate than mathematical terminology used poetically in verbal theorizing: Fourier Series and related techniques enable one to represent quite varied function forms -- straight lines, exponential growth or decay, damped oscillations, continuing oscillations, etc. -- all in terms of the cyclical functions, sine and cosine. Even in verbal formulations, expressions such as "Dawn of a New Day" and "Next Year in Jerusalem" simultaneously evoke both cycles and anticipation of progress.

Clearly, calendar systems have been many and varied. But not all of the calendar systems worked equally well, in the sense of accurately keeping track of important recurrences, while maintaining ease of use. A couple of deficiencies were common:

An ideal calendar, then, would be both accurate and easy to use, and in fact widely accessible.

The following, unless explicitly stated otherwise, pertains to the calendar used in the contemporary United States and much of the world. This calendar has some practical advantages, and not just European imperialism, to help explain its widespread adoption. It is sufficiently accurate to get crops planted in the appropriate season, and is simple enough to be used by people who are unable to set the correct date and time in a computer or VCR, and who need to be reminded about daylight saving time, but who can usually figure out which days they don't have to go to work.

Time (as in years and millennia) is measured on what social researchers call an "interval scale": it has a meaningful unit of measurement, but an arbitrary zero point.

Time on Very Long and Short Scales

The above is concerned with time on a long scale -- years, centuries, millennia -- as is appropriate on a web page about millennial matters. In this section, I will just briefly mention a couple of issues and references pertaining to conceptualization and measurement of time on scales which are even longer, or else considerably shorter. The final section on time will be devoted to months and, especially, weeks.

Geologists deal with even longer time frames, and draw on the physics of radioactivity for geological dating in millions rather than thousands of years. Elsewhere in physics, cosmologists (with more than a bit of resemblance to theologians) trace their version of time clear back to a "big bang" at the creation of the universe. There are popular accounts at least some of which are by acknowledged experts (Harbaugh, Hawking, Morris, Wald). However, the cosmologists' time frame is so much different from that of years or millennia that I am not sure there is any useful carryover.

In this Millennium web page I will not go into any detail concerning issues of time on even shorter scales, of days, hours, minutes, and fractions thereof, nor on instruments used to measure such. Time on such small scale is a much more complex topic (Davis and Foote; Waugh, esp. chapter 2; Seidelmann, esp. chapter 2). The illiterate shepherd who needed only his eyes to observe the waxing and waning of the moon phases would likely have been clueless about minutes and seconds, let alone nanoseconds.

Instrumentation and theories (social constructs, both) are crucial here. Much important instrumentation was developed either to measure time per se, or to measure time as a step toward measuring location, particularly longitude of ships at sea. Holbrook (also see Turner) discusses such historical instruments as the astrolabe, the quadrant, and the universal equinoctial ring dial, which were used to measure time by the angular positions of sun or stars. The transit, still in use by surveyors, can be used similarly (Breed and Hosmer). The theory and construction of sundials is a topic to which Waugh devotes an entire book (which may seem like overkill until one reads, page vii, that Waugh's personal library contains "well over one hundred old books on sundials, many of them beautifully bound and illustrated"). Sobel provides an accessible account of the development of the marine chronometer, and gives further references.

Time on the hours-and-minutes scale would seem to be of some sociological importance, having been crucial in regimenting the workforce required in the development of industrial capitalism.

Months and Weeks

In discussions of time on a long scale, the most relevant readily observed natural periodicity is that of the seasons. The seasons themselves (although not their precise lengths) were readily observable in zones away from the equator. No special knowledge or equipment was required. The simplest herder or hunter, with no theories from astrology, astronomy, theology, etc., with no special equipment such as telescopes or thermometers and nothing more than his ten fingers for calculations, could still recognize the repeated cycles of seasons, with such features as warmth and cold, leaves growing and falling, snow accumulating and melting. In a climate with less distinct seasons, the ancient Egyptians could readily observe the annual flooding of the Nile, long before they knew about the more pronounced seasons upstream.

For durations of time shorter than a year, other readily observed natural periodicities are on more suitable scales. The week approximates one phase of the moon, and the month their repetition in cycles of four phases. The periodicity of light and darkness form day and night. These too are readily observable by ordinary people, not requiring any special equipment nor theories from theology, astrology, or whatever.

Furthermore, even "readily observable" is not strong enough a description. Prior to the widespread deployment of street lights, even city dwellers, when they were outdoors after sundown, found the moon's phases a dramatic spectacle impossible to overlook, and that is still the case in suburban and rural areas.

I am quite unconvinced by Zerubavel's (page 11; emphasis in original) characterization of the 7 day week as "an entirely artificial mathematical rhythm ... totally independent of the lunar or any other natural cycle", and based primarily on theological rather than astronomical considerations. (He argues that development of a 7 day week was aimed at establishing the Jewish god as "supranatural" and thus superior to the "natural" gods identified with the sun or moon.)

Perhaps Zerubavel was merely overstating his position to make a point, a not uncommon practice. But taken literally, his description of "an entirely artificial mathematical rhythm" does not fit the 7 day week nearly as well as it fits the failed attempt during the French revolution to institute a 10 day week (pages 28 ff).

The complexities of calendars (notably leap years) arise largely from the fact that the most obvious natural periodicities are not integer multiples of each other: There are some 7 and a fraction (not exactly 7) cycles of light and darkness in one of the moon phases, and some 29 and a fraction of them in a cycle of the four moon phases. Likewise, there are some twelve and a fraction (not exactly 12) moon phase cycles in one cycle of the seasons.

Any ancient hunter or herdsman, unschooled in astrology or theology, with no knowledge of the number of planets found by astronomers, the number of days of creation posited by theologians, or the number of astrological signs, and with only his fingers for computations, could, without any special equipment or theories, clearly see the phases of the moon and discern that each lasts about 7 days.

What was left for "social construction" is not whether the week would have 7 or 10 days; that came from a highly visible, easily interpreted natural regularity of moon phases. Rather, what was left for "social construction" was just what to do with the fractions of days left over, when the learned priests and astronomers tried to reconcile the periodicity of moon phases with the periodicity of other natural phenomena.

Analogous to what is done with February 29 on leap years, one might imagine a calendar system in which some "Specialday" (or perhaps "Jubileeday") would from time to time be inserted, say between Saturday and Sunday, to bring the week back into synchronization with lunar months. Such an arrangement would have weeks usually of 7 days, but occasionally of 8 days instead. But that is not done in our calendar. Rather, the regular cycling of Sunday, Monday, ..., Saturday (and starting over with Sunday again) continues indefinitely, every 7 days, with no interruptions.

(A note on Jubilee Year: Although repeatedly referencing the biblical significance of the number 7, Zerubavel fails to mention the way Leviticus tells to order YEARS, not by uninterrupted multiples of 7, but by 50s, the latter consisting of 7 times 7, plus one additional year, the Jubilee, devoted to various sorts of special celebration, including the forgiving of debts. Now why, one might ask, was it so important for days, but not years, to follow uninterrupted repetition in multiples of seven? Not from either version of the creation story, where one finds nothing about the 8th day being a repetition of the first, the 9th a repetition of the 2nd, etc.)

Zerubavel takes particular notice of the way those unsynchronized periodicities were resolved, without disrupting the regular succession of the 7 days. Although also noting inconveniences due to lack of coordination of weeks with other time units (e.g., a monthly paycheck covering 4 weeks' groceries some months, 5 weeks' groceries other months; page 60) Zerubavel emphasizes the regularly recurring 7 day week's importance for "the establishment of settled life with a high level of social organization, particularly significant since the rise of a market economy, which involved orderly contact on regularly recurrent, periodic market days" (page 10).

I concur with Zerubavel on that point. Now if only he could come up with a way to rationalize those pesky holidays, which disrupt Thursday and Friday classes fall term, and Monday classes winter term!

References:

Bourgeois, Julia F. 1942. "The True Calendar-Years of Aztecs and Mayas and the True Mayan Calendar System." Revised edition of paper presented at the xxvi International American Congress in Seville, October 12, 1935. Mexico, D. F.: Editorial Cvltvra.

Brainerd, George W. 1954. The Maya Civilization. Los Angeles: Southwest Museum. Pages 42-49, "Calendrics".

Breed, Charles B., and George L. Hosmer 1934. The Principles and Practice of Surveying. Volume II: Higher Surveying. Fourth 2edition. New York: Wiley. Pages 101-109, "Time".

Cajori, Florian 1931. A History of Mathematics. New York: Macmillan. Pages 69-70, "The Maya", plus material on several other calendars.

China Science and Technology Museum 1983. China: 7000 Years of Discovery: China's Ancient Technology. San Francisco: China Books.

Cowan, Harrison J. 1958. Time and Its Measurement. Cleveland: World Publishing Co.

Davis, Raymond E., and Francis S. Foote 1953. Surveying: Theory and Practice. New York: McGraw-Hill. Chapters 20, 21.

Dilke, O. A. W. 1987. Mathematics and Measurement. Berkeley: University of California Press.

Doggett, L. E. 1992. "Calendars." Chapter 12, pp. 575-608, in Seidelmann (1992).

Duncan, David Ewing 1998. Calendar: Humanity's Epic Struggle to Determine a True and Accurate Year. New York: Avon Books.

Eves, Howard 1990. An Introduction to the History of Mathematics. With Cultural Connections, by Jamie H. Eves. 6th edn. Orlando: Harcourt Brace.

Garcia Valades Editores [no date]. Aztec Calendar, History and Symbolism. (Booklet with large fold-out illustrations.) Mexico D. F.: Garcia Valades Editores.

Gould, Stephen Jay 1997. Questioning the Millennium: A Rationalist's Guide to a Precisely Arbitrary Countdown. New York: Harmony Books.

Harbaugh, John W. 1968. Stratigraphy and Geologic Time. Dubuque IA: William C. Brown.

Hawking, Stephen W. 1988. A Brief History of Time: From the Big Bang to Black Holes. New York: Bantam.

Klein, Herbert Arthur 1974. The Science of Measurement: A Historical Survey. New York: Dover.

Morris, Richard. 1985. Time's Arrows: Scientific Attitudes Toward Time. New York: Simon and Schuster.

Robinson, Andrew 1995. The Story of Writing. London: Thames and Hudson. Ch. 7, "Mayan Glyphs".

Rubin, Arnold. 1989. Art As Technology. Beverly Hills CA: Hillcrest Press.

Seidelmann, P. Kenneth, ed. 1992. Explanatory Supplement to the Astronomical Almanac. Mill Valley, CA: University Science Books.

Smith, David E. 1958. History of Mathematics. 2 vols. New York: Dover.

Sobel, Dava 1995. Longitude: The True Story of a Lone Genius Who Solved the Greatest Scientific Problem of His Time. New York: Walker and Co.

Turner, Gerard L'E. 1998. Scientific Instruments 1500-1900. Berkeley and Los Angeles: University of California Press.

Wald, Robert M. 1977. Space, Time, and Gravity: The Theory of the Big Bang and Black Holes. Chicago: University of Chicago Press.

Waugh, Albert E. 1973. Sundials: Their Theory and Construction. New York: Dover.

Zerubavel, Eviatar 1989. The Seven Day Circle: The History and Meaning of the Week. Chicago: University of Chicago Press.

Millennial Orthography and Etymology